Recursive Update Filtering: A New Approach
Consider the data assimilation (or measurement update problem): given a prior state estimate with an associated uncertainty distribution, incorporate new information from a measurement. This new information should nudge the state estimate closer to the true state and reduce uncertainty.
If the measurement is a nonlinear function of the state, the state update can be computed using the Extended Kalman Filter (EKF) equations.
\[\hat{x} = \bar{x} + K*(y - h(\bar{x}))\] \[\hat{P} = (I - KH)\bar{P}\] \[K = \bar{P}H^T(H\bar{P}H^T + R)^{-1}\]where \(H\) is the measurement Jacobian
\[H = \frac{\partial h}{\partial x}.\]\(H\) contains the set of derivatives of the measurement model \(y = h(x) + \eta\) with respect to the states. The measurement has its own uncertainty, \(\eta \sim \mathcal{N}(0,R)\). The figure below shows the result of the EKF update for a range measurement.
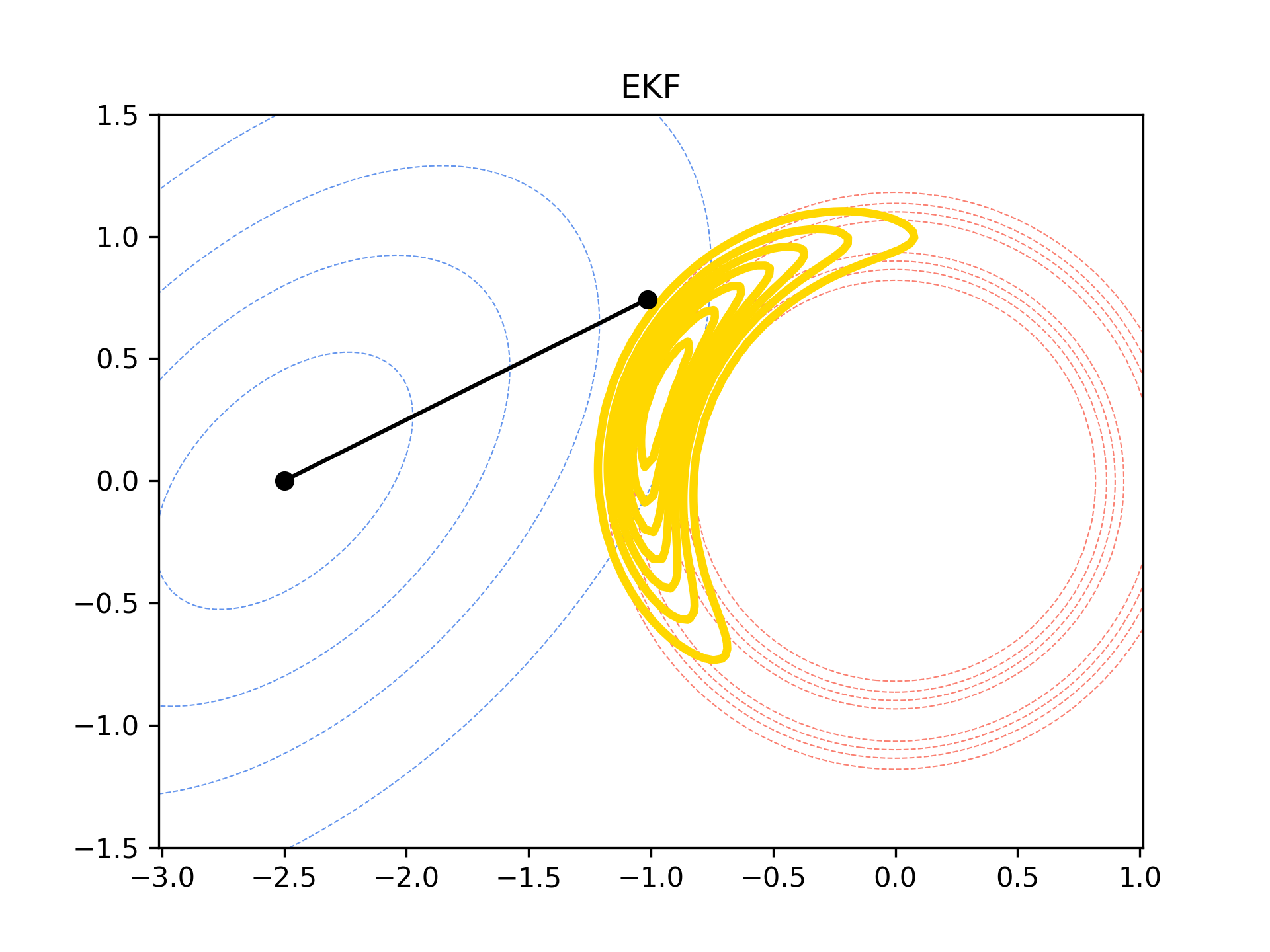
In this figure, the prior state estimate is \(\hat{x} = \begin{bmatrix} -2.5 & 0 \end{bmatrix}\). The prior distribution is Gaussian and centered at the prior state estimate. The measurement model is,
\[h(x) = \sqrt{x_1^2 + x_2^2},\]the distance of the state from the origin. The measurement uncertainty is \(R = 0.1^2\). This forms a measurement likelihood distribution in the shape of a ring (red) with maxima at the measurement value, \(y = 1\). The crescent-shaped posterior distribution, the distribution we’re hoping to capture with our EKF update, is shown in yellow.
The updated state estimate lies close to the posterior distribution. But we can do better!
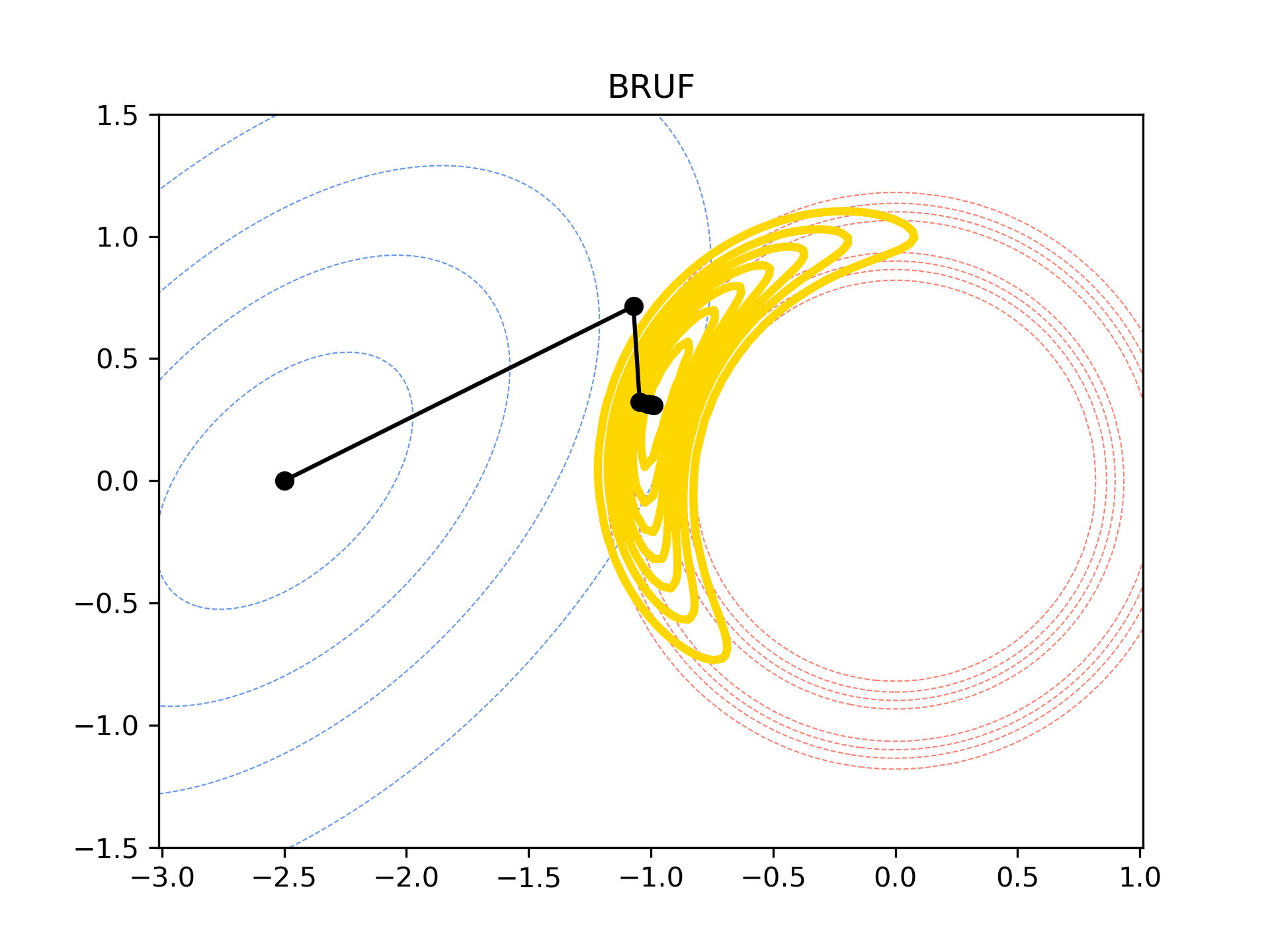
Consider the Bayesian Recursive Update Filter (BRUF), in which we apply the EKF update \(N\) times with inflated measurement noise covariance \(NR\).
\[\hat{x}_{i+1} = \hat{x}_i + K_i*(y - h(\hat{x}_i))\] \[\hat{P}_{i+1} = (I - KH_i)\hat{P}_{i+1}\] \[K_i = \hat{P}_iH_i^T(H_i\hat{P}_iH_i^T + NR)^{-1}\]where \(\hat{x}_{0} = \bar{x}\), \(\hat{P}_0 = \bar{P}\), and \(H_i = \partial h / \partial (\hat{x}_i)\).
The intuition behind the BRUF is that by inflating the measurement noise covariance to \(NR\), we trust the measurement less than we would have in a single EKF update. The figure below shows the result of \(N=5\) BRUF updates for the range measurment. Interestingly, even with relatively few steps, the state estimate approaches the maximum a posteriori (MAP) estimate, the maximizer of the posterior distribution.
In later work, we presented a continuous formulation of the BRUF update. In this version, the following set of differential equations is solved on the interval \(\tau \in [0,1]\).
\[\dot{\hat{x}} = \hat{P}H^TR^{-1}(y - h(\hat{x}))\] \[\dot{\hat{P}} = - \hat{P}H^TR^{-1}H\hat{P}\]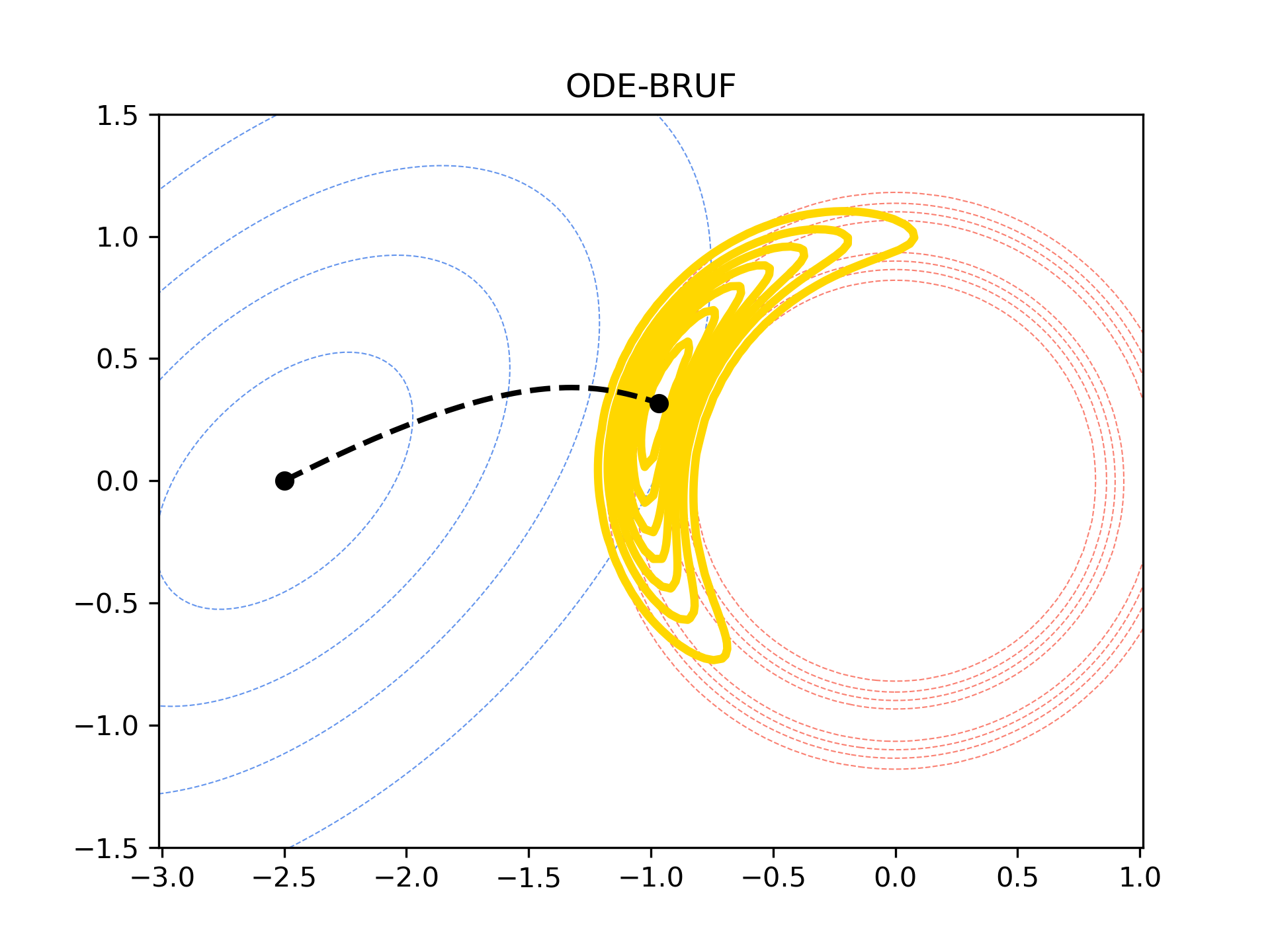
We can also extend the continuous-time BRUF update to particle and ensemble filtering. In the figure below, the update is applied to a set of particles sampled from the prior distribution (o). The updated particles (•) fall nicely on the posterior distribution.
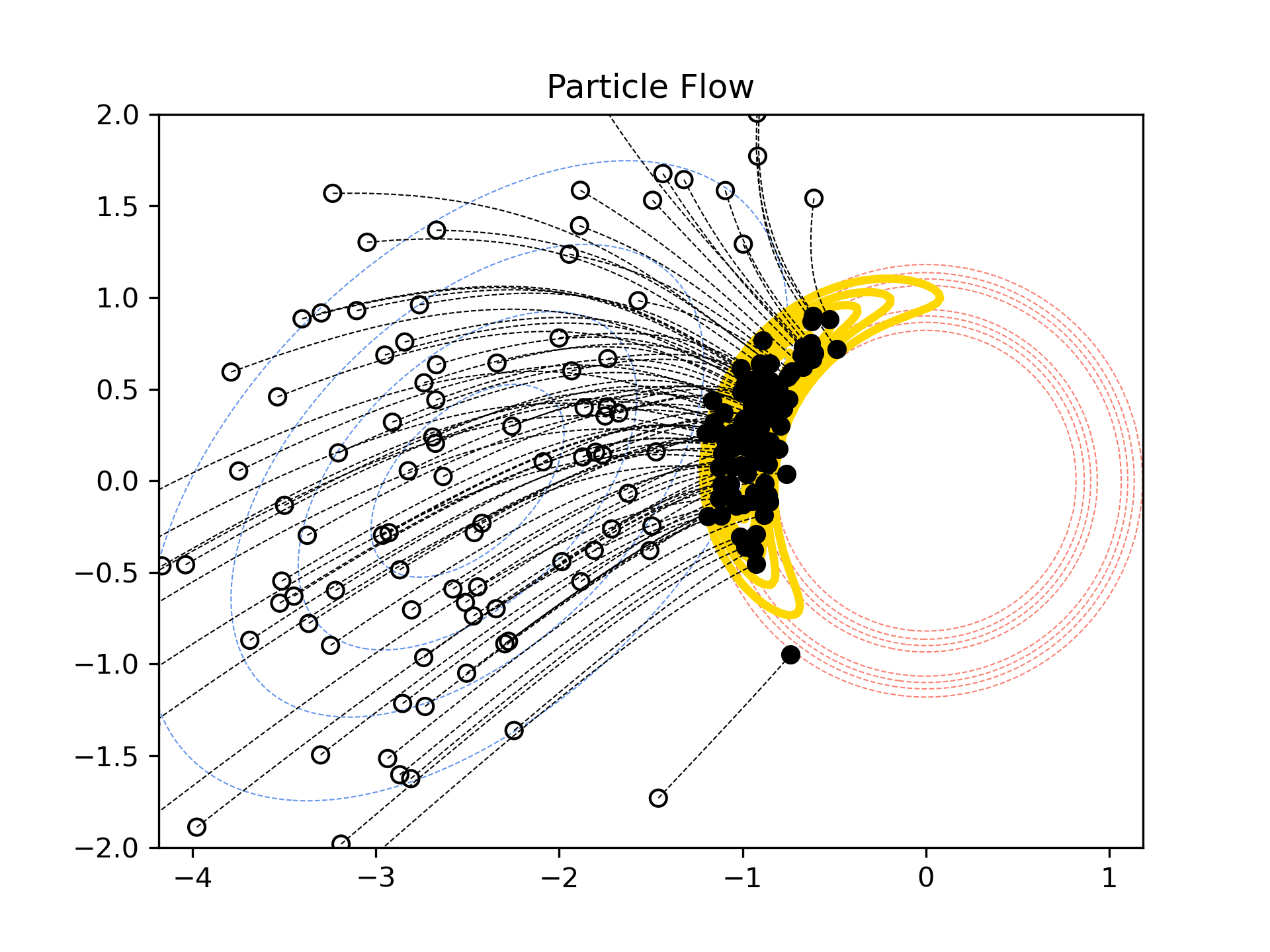
Code for these examples is available on Github.
Selected References
Kristen Michaelson, Andrey A. Popov, and Renato Zanetti. “Recursive Update Filtering: A New Approach.” AAS Space Flight Mechanics Conference. Austin, TX. January 15-19, 2023.
Kristen Michaelson, Andrey A. Popov, Renato Zanetti, and Kyle J. DeMars. “Particle Flow with a Continuous Formulation of the Nonlinear Measurement Update.” 27th International Conference on Information Fusion. Venice, Italy. July 7-11, 2024.
Kristen Michaelson, Andrey A. Popov, and Renato Zanetti. “Multiple Data Assimilation as an Approximate Maximum a Posteriori Estimator.” Computational Geosciences. April 2025.
